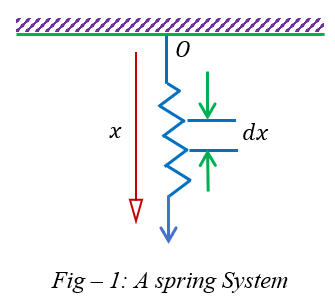
Statement: Derive the expression of Potential Energy stored in a spring, `U = \frac{1}{2} k x^2`
Solution:
Elastic potential energy (U)
is potential energy stored as a result of deformation of an elastic object,
such as the stretching of a spring. It is equal to the work done (W) to stretch
the spring, which depends upon the spring constant k as well as the distance
stretched i.e. U = W
Let the spring be stretched trough a small distance `dx`. Then work done in stretching the spring through a distance `dx` is,
`dW = F dx` ...................................... (1)
Where, F is the force applied to the
stretch the spring.
Total work done in stretching the spring from the interval `x = 0` to `x = x` is obtained by integrating the expression:
`\int dW=\int_{0}^{x}Fdx`..............................(2)
Hooke’s Law states that, the elongation produced in an ideal spring is directly proportional to the spring force. That is,
`F = - kx` ......................................(3)
Here,
k is called the spring constant.
Substituting equation (iii) in (ii) we get,
Work done by spring force,
`W=\int_{0}^{x} -kxdx=-k\int_{0}^{x}xdx=-k [\frac{x^2}{2}]_0^x=-\frac{1}{2}kx^2` ............................ (4)
And the work done by external force = `\frac{1}{2} kx^2`
This work done to deform the spring is nothing but the elastic potential energy of the spring.
Hence, `U = \frac{1}{2} k x^2`
[Derived/Proved]