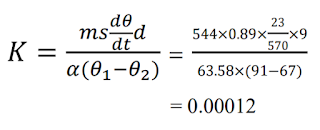${tocify}
Abstract
The co-efficient of thermal conductivity of bad conductor’s is determined by taking the specimen
in the form of a flat disc. The experimental disc is sandwitched between a metallic heavy
bottomed cylindrical steam chamber and a brass disc. The whole assembly is suspended from a
heavy retort stand. The lower part of the chamber and the disc are varnished and carry mercury
thermometers and respectively inserted in the holes drilled in them. In order to perform the
experiment, steam is passed through the chamber and the temperatures shown by the
thermometer and are recorded turn by turn until they become steady. In this steady state, the
arte of heat conducted through the experimental disc is equal to the rate of heat radiated from
the exposed surface of the disc [1].
Introduction
Thermal conductivity: In general, good conductors of electricity (metals like copper,
aluminum, gold, and silver) are also good heat conductors, whereas insulators of electricity (wood,
plastic, and rubber) are poor heat conductors. The figure below shows molecules in two bodies at
different temperatures. The (average) kinetic energy of a molecule in the hot body is higher than
in the colder body. If two molecules collide, an energy transfer from the hot to the cold molecule
occurs. The cumulative effect from all collisions results in a net flux of heat from the hot body to
the colder body. We call this transfer of heat between two objects in contact thermal conduction
[2].
Fig. 01 (The molecules in two bodies at different temperatures have different average kinetic
energies. Collisions occurring at the contact surface tend to transfer energy from high-temperature regions
to low-temperature regions)
Bad conductor: Bad conductors are materials/matter that can conduct heat and electricity
partially or in most cases, doesn't conduct heat and electricity at all. Bad (weak conductors) are
usually non-metal elements and compounds such as water (H2O), plastic and paper. Although,
there are some covalent molecules that conduct electricity in aqueous state such as aqueous
hydrochloric acid, HCl as there are free moving ions in the solution [3].
Specific heat: The specific heat is the amount of heat per unit mass required to raise the
temperature by one degree Celsius. The relationship between heat and temperature change is
usually expressed in the form shown below where c is the specific heat [4].
The relationship between heat and temperature change is usually expressed in the form shown
below where c is the specific heat. The relationship does not apply if a phase change is
encountered, because the heat added or removed during a phase change does not change the
temperature.
LEE’s disc experiment: The Lee’s disc experiment is used to determine an approximate value
for the thermal conductivity K of a poor conductor like glass, cardboard etc.
The procedure is to place a disc made of poor conductor, radius r, and thickness x, between a
steam chamber and two good conductivity metal discs (of the same material).
The formula here used is,
Theory
The thermal conductivity of a bad conductor like rubber, glass, leather, cardboard, ebonite etc. can
be determined by Lee’s method. In measuring the conductivity of such a poor conductor one much
remember that a this layer of slab of the material must be used. The difficulty then arises in
maintaining the face at uniform temperature and this measuring that temperature.
Lee’s and Charlton overcome this difficulty by placing a slab of a good conductor, such as brass
or copper, of exactly same diameter. A and C are metallic placed over and under the disc S.
If,
ϴ1 = Temp of B in the steady state,
ϴ2 = Temp of A in the steady state,
α = Area of the cross section of the slabs,
K = Thermal conductivity,
D = Thickness of the slabs.
Then the quantity of heat conducted per second through the poorly conducting slab S is,
Where, m - mass of the brass disc
s - specific heat capacity of brass.
From eqn
(1) and (2) we get,
Apparatus
1. Lee's disc apparatus
2. a brass disc and a metallic disc of large diameter compared to its thickness
3. sample of bad conductor in the form of the disc with same diameter
4. two mercury thermometers
5. stop watch
6. vernier
7. screw gauge and
8. a balance.
Experimental data
Table for determining time temperature record A & B
Table: time temperature record of A during its cooling
Calculation
Where,
Mass of the metal disc A, m = 544 gm
Mass of the metal disc A, m = 544 gm
Specific heat of the material of metal disc As = 0.089KJ/Kg/K
Diameter of the specimen slab S, d = 9 cm
Area of cross-section, α = π×(0.273)×2 sq. cm = 63.58
Thickness of the specimen slab S, d = 2.5+23×.01=.273 cm
From the cooling graph the slope of the tangent,
dϴ/dt = 0.0426
ϴ1 - ϴ2 = (91-67) = 24
Percentage of error
Result
The thermal conductivity of a bed conductor is 0.00012 calories per cm per sec per ℃ with an
error of 71.831%
Discussion
Temperature ϴ1 and ϴ2 of B and A noted when they remain steady for at least 10 to 15 minutes.
Every data which is significant to the experiment noted during the observation.
For ensuring an uniform and good emissivity, the surface of A and B should be nickel plated. The
discs B, S and A are tight plated together so that there is no air between them.
During cooling the temperature of the lower disc A might be noted every half minute or more to
ensure less error or more efficiency.
A non-luminous flame might be used to heat so that the emissivity or the surface does not change
by the deposition of shoot on it.
The temperatures may be placed close to the faces of S, one on either side. Ensuring a good
observation, promises better result.
Conclusion
From the experimental results, the value of the thermal conductivity of the materials selected was
low; this is because they are all non-metals with high insulating value. Thermal conductivity is
regarded as the most important characteristic of a thermal insulator since it affects directly the
resistance to transmission of heat that a material offers. The lower the thermal conductivity value,
the lower the overall heats transfer. Comparing the result with other thermal insulators as reported
by other researchers who have carried out similar experiment, it was evident that the modified
apparatus has some measurable degree of effectiveness considering the fact that the differences
in the value obtained was between 1.0-8.0 percent.