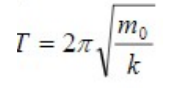Abstract
Firstly, we measure the diameter of the spring several times using slide calipers and take the
mean value. Then we attach it to a stand. Diameter of the wire is then measured by screw gauge.
Then twice the diameter of wire is substracted from outer diameter of spring to get inner
diameter and average of that two is taken as diameter of spring.[1] Now a certain mass is hung
from spring. Mean position is marked. We lift it and let go causing a vertical oscillation. We
measure the time for 50 oscillation and record the corresponding data. The same process is
repeated for 5 times. Then graph plotting (T^2
vs M) ,calculation of k and and error analysis is
done based on the obtained data.
Introduction
Spring constant is a
characteristic of a spring which is defined as the ratio of the force
affecting the spring to the displacement caused by it. Usually denoted with the
letter "k" in formulae, as in the formula F =k − x , where "F"
is the force applied and "x" is the displacement. Hooke's Law states
that the restoring force of a spring is directly proportional to a small
displacement.[2] In equation form, we write,
Where x is the size of the displacement. The proportionality constant k is specific for each
spring. The object of this virtual lab is to determine the spring constant k.[3]
The effective mass of the spring in a spring-mass system when using an ideal spring of
uniform linear density is 1/3 of the mass of the spring and is independent of the direction of the
spring-mass system (i.e. horizontal, vertical, and oblique systems all have the same effective
mass). This is because external acceleration does not affect the period of motion around the
equilibrium point.
We can find the effective mass of the spring by finding its kinetic energy. This requires adding
all the mass elements' kinetic energy, and requires the following integral, where u is the velocity
of mass element :
Modulus of Rigidity, G: Modulus of rigidity of a spring is
also known as the spring constant (Shear Modulus) is the coefficient of
elasticity for a shearing force. It is defined as "the ratio of shear
stress to the displacement per unit sample length (shear strain)".Modulus
of Rigidity can be experimentally determined from the slope of a stress-strain
curve created during tensile tests conducted on a sample of the material. The
definition of Modulus of Rigidity: the ratio of shear stress to the
displacement per unit sample length (shear strain).[5]
Theory
In this experiment a spring is suspended vertically from a clamp attached to a rigid frame work
of heavy metal rods. At the bottom end (which is the free end) of the spring a load of
mass, m0 is suspended. So the force acting on the spring is the weight m0g of the load
which acts vertically downward and the spring gets extended. Due to the elastic property
of the spring, it tries to regain its initial size, hence applies a counter force on the load,
which is called the restoring force of the spring. According to Hooke’s law, magnitude of this
restoring force is directly proportional to the extension of the and the direction of this restoring
force is always towards the equilibrium position.[6] If k is the spring constant of the spring and
the extension of the spring, then restoring force = - kl
Let the spring is in equilibrium with mass mo
attached as in Fig. 02 (a), and so we can write
m0g = kl
=> l=g/k mo … … … …
… … … … … … … … …(1)
Here,
k is the
spring constant and g is the acceleration due to gravity.
Equation (1) is an equation of straight line slope of this
line is given by
Slope = g/k,
K = g/slope
… … … … … … … … … … … … …(2)
We can plot l vs mo graph and determine its
slope to determine k
If the load is slightly pulled down and released, the
spring will oscillate simple harmonically. Suppose, at time t the velocity of
the load is v and the spring is compressed by a distance y above the point C.
As we know from our earlier schools if the mass of the spring were negligible
then the period of oscillation.
That would be given by,
Due to the mass, m of the spring an extra term m′ will be added with the mass of the load mo in
the above mentioned equation. So, the period of oscillation is,
m′ is called to be the effective mass of the spring. It can be showed that m′ is related with the
mass of the spring by following equation,
m' = m/3 … … …. …. …. … … … … … … … … … … … (4)
So, from equation (3), we get,
For different mass, mo of the load we find
different periods of oscillation, T. If we draw a graph by plotting m0
along X axis and corresponding T2 along Y axis, it will be a
straight line. The point where the line intersects the X axis, its y-coordinate
is 0, i.e. T2 = 0 there. We can find the X coordinate of the point,
(i.e. the value of mo at that point) by putting T2 = 0 in
the above mentioned equation,
That means x coordinate of the point is equal to the
negative value of the effective mass. So, if we draw a T2 vs. mo
graph, it will be a straight line and its x-interception gives us the effective
mass of the spring.
If n is the rigidity modulus of the material of
the spring than it can also prove that,
Where,
N = Number of turns in the spring
R =
Radius of the spring
K = Spring constant
r = Radius of the wire of the spring
Apparatus
1. A
spiral spring
2.Convenient
masses with hanging arrangement
3.Clamp
or a hook attached to a rigid framework of heavy metal rods
4. Weighting
balance
5. Stop
watch and
6. Scale
Experimental Data
|
No. of observation
|
Loads mo in gm
|
Extension in cm
|
No. of vibrations
|
Total time in sec
|
Period T in sec
|
T2
|
|
|
0
|
15.9
|
|
------
|
------
|
-----
|
|
1
|
50
|
6.1
|
50
|
50.80
|
1.016
|
1.032
|
|
2
|
100
|
12.6
|
50
|
56.77
|
1.1354
|
1.289
|
|
3
|
150
|
18.9
|
50
|
61.03
|
1.2306
|
1.514
|
|
4
|
200
|
25.3
|
50
|
68.72
|
1.3744
|
1.888
|
|
5
|
250
|
31.2
|
50
|
70.59
|
1.4118
|
1.9931
|
Calculation
Spring constant, K = Mg = 7229.508 dynes/cm
From graph (2) effective mass = 40 gm
a) No.
of turns N in the spring = 162
b) Radius
of the spring, R = (D+d)/4 = (2.785+2.575)/4 = 1.34 cm
c) Radius
of the wire of the spring, r = 0.65975 cm
Percentage error
Result
The spring constant of a given spiral spring is
7229.508 dynes/cm and effective mass is
40 gm. And the rigidity modulus of the material of the spring is 8.8439 × 10^11 dynes/cm with an error of 6.5% .
Discussion
Measurement
of radius of wire/spring and weight-
1. Some instrumental error may arise if main scale
zero doesn’t coincide with circular scale
zero. That have been taken care of by adding or substracting the error.
2. If the wire is not uniform then readings have to
take at different points and mean of them is
the best reading.
3. While hanging the weights that should lie along
the axis of spring. This doesn’t occur during experiment.
Measurement
of time period -
1. Firstly
measurement of time period is not accurate due to personal observation error.
2. Oscillations
should occur in vertical plane but it oscillates little in a horizontal plane
also.
Conclusion
In the experiment, there are some important apparatus.
These apparatus are very useful to find out the exact value of spring material.
Spring constant can be measured accurately by following the precaution of these
apparatus. There will be small amount of error if the value is taken
accurately.
References
[1].https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0ahUKEwj60aSM8sfVAhWLrY8KHeUTCbIQFggnMAA&url=http%3A%2F%2Fwww.cmi.ac.in%2F~souvik%2Flab3%2Fspr.pdf&usg=AFQjCNGRt2dLUl2AUz oE9PnZ-ZukensdYg
[2].https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0ahUKEwj60aSM8sfVAhWLrY8KHeUTCbIQFggvMAE&url=http%3A%2F%2Fkamaljeeth.net%2Fnewsite%2Findex.php%3Froute%3Dproduct%2Fproduct%2FgetProductAttachmentFile%26attachment_id%3D301&usg=AFQjCNHiQGpibxIrHE3VmtBLZXEl-PLw4Q
[3]. https://www.coursehero.com/file/8113988/EXP4/
[4].http://www.markedbyteachers.com/as-and-a-level/science/the-experiment-involves-thedetermination-of-the-effective-mass-of-a-spring-ms-and-the-spring-constant-k.html
[5]. https://mainulgub.files.wordpress.com/2016/06/scan0002.pdf
[6]. http://ncert.nic.in/ncerts/l/kelm105.pdf